Capgemini Assessment Pattern & Flow
Video Tutorial: Complete Assessment Guide
Watch this comprehensive tutorial to understand the complete Capgemini assessment process:
Pro Tip: Subscribe to our Learning Unique channel for more coding tutorials and assessment guides!
Assessment Completion Pattern
Click on the image below to view it in full screen and understand the complete assessment flow:

Key Points:
- ? Assessment Duration: 40 minutes for coding section
- ? Max Score: 05 marks total
- ? Question Pattern: 2 coding problems (as shown in next sections)
- ? Time Management: ~20 minutes per question is recommended
- ? Success Tip: Practice both problems multiple times before the actual assessment
Coding Questions Asked on September 17, 2025
Select a problem by clicking on the boxes below to view descriptions and solutions. These questions were asked on September 17, 2025.
Q2. Deleting a Subsequence - Coding Question Asked on
String ManipulationChallenge: Remove "AB" and "CD" subsequences to minimize string length
Concept: Stack operations and pattern matching
? Difficulty: Medium
Q1. Sum of Remainders - Coding Question Asked on
MathematicalChallenge: Calculate sum of remainders for consecutive divisions
Concept: Modular arithmetic and optimization
? Difficulty: Medium
Click on any question box above to view the complete problem statement, solution approach, and multi-language code implementations!
Coding Questions Asked on September 22, 2025
Select a problem by clicking on the boxes below to view descriptions and solutions. These are the latest questions asked on September 22, 2025.
Q1. Array Balance Point - Array Manipulation Challenge
Array ManipulationChallenge: Find balance point where left sum equals right sum
Concept: Prefix sums and efficient array traversal
? Difficulty: Medium
Q2. Array Out of Bounds - Simulation Challenge
Array SimulationChallenge: Count steps until array goes out of bounds
Concept: Array traversal with alternating left-right movement
? Difficulty: Medium
Click on any question box above to view the complete problem statement, solution approach, and multi-language code implementations!
Q1. Array Balance Point - Find Left Sum = Right Sum Latest Sept 22
Problem Overview:
This is an array manipulation challenge that tests your understanding of prefix sums and efficient array traversal. You need to find the balance point where the sum of elements on the left equals the sum of elements on the right.
Key Concepts:
- Prefix Sum: Calculate cumulative sums efficiently
- Balance Point: Find index where left_sum = right_sum
- Array Traversal: Single pass optimal solution
- Mathematical Approach: Total sum - current element = 2 * left_sum
Algorithm Strategy:
Calculate total sum first, then traverse the array maintaining left_sum. At each position, check if left_sum equals (total_sum - current_element - left_sum). This gives us the balance point efficiently!
Q1. Array Balance Point - Find Left Sum = Right Sum
You are given an array of integers. Find the balance point (index) where the sum of elements to the left equals the sum of elements to the right. If no such point exists, return -1.
Problem Understanding:
- ? Find index i where sum(arr[0...i-1]) = sum(arr[i+1...n-1])
- ? The element at index i is not included in either sum
- ? Return the first such balance point if multiple exist
- ? Return -1 if no balance point exists
Input Format
The input consists of two lines: The first line contains an integer `N`, and the second line contains `N` space-separated integers representing the array.
Output Format
Print the index of the balance point (0-based), or -1 if no balance point exists.
Constraints
1 ≤ N ≤ 105
-109 ≤ arr[i] ≤ 109
Example
Input:
7
1 2 3 4 3 2 1Output:
3Step-by-Step Solution:
Array: [1, 2, 3, 4, 3, 2, 1] (Total sum = 16)
Check each index:
Index 0: Left: [] = 0, Right: [2,3,4,3,2,1] = 15 ?
Index 1: Left: [1] = 1, Right: [3,4,3,2,1] = 13 ?
Index 2: Left: [1,2] = 3, Right: [4,3,2,1] = 10 ?
Index 3: Left: [1,2,3] = 6, Right: [3,2,1] = 6 ?
Answer: Index 3 is the balance point where left sum equals right sum!
Additional Test Cases
Test Case 2:
Input:
5
1 2 3 2 1Output:
2Explanation: At index 2, left sum = 1+2 = 3, right sum = 2+1 = 3
Test Case 3:
Input:
4
1 2 3 4Output:
-1Explanation: No balance point exists in this array
Test Case 4:
Input:
3
5 0 5Output:
1Explanation: At index 1, left sum = 5, right sum = 5
Test Case 5:
Input:
1
10Output:
0Explanation: Single element array always has balance point at index 0
#include <iostream>
#include <vector>
using namespace std;
int findBalancePoint(vector<int>& arr) {
int n = arr.size();
if (n == 0) return -1;
if (n == 1) return 0;
// Calculate total sum
long long totalSum = 0;
for (int i = 0; i < n; i++) {
totalSum += arr[i];
}
long long leftSum = 0;
for (int i = 0; i < n; i++) {
// Right sum = totalSum - leftSum - arr[i]
long long rightSum = totalSum - leftSum - arr[i];
if (leftSum == rightSum) {
return i;
}
leftSum += arr[i];
}
return -1;
}
int main() {
int n;
cin >> n;
vector<int> arr(n);
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
cout << findBalancePoint(arr) << endl;
return 0;
}import java.util.*;
public class ArrayBalancePoint {
public static int findBalancePoint(int[] arr) {
int n = arr.length;
if (n == 0) return -1;
if (n == 1) return 0;
// Calculate total sum
long totalSum = 0;
for (int i = 0; i < n; i++) {
totalSum += arr[i];
}
long leftSum = 0;
for (int i = 0; i < n; i++) {
// Right sum = totalSum - leftSum - arr[i]
long rightSum = totalSum - leftSum - arr[i];
if (leftSum == rightSum) {
return i;
}
leftSum += arr[i];
}
return -1;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = scanner.nextInt();
}
System.out.println(findBalancePoint(arr));
scanner.close();
}
}#include <stdio.h>
int findBalancePoint(int arr[], int n) {
if (n == 0) return -1;
if (n == 1) return 0;
// Calculate total sum
long long totalSum = 0;
for (int i = 0; i < n; i++) {
totalSum += arr[i];
}
long long leftSum = 0;
for (int i = 0; i < n; i++) {
// Right sum = totalSum - leftSum - arr[i]
long long rightSum = totalSum - leftSum - arr[i];
if (leftSum == rightSum) {
return i;
}
leftSum += arr[i];
}
return -1;
}
int main() {
int n;
scanf("%d", &n);
int arr[n];
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
printf("%d\n", findBalancePoint(arr, n));
return 0;
}Q2. Array Out of Bounds - Simulation Challenge Latest Sept 22
Problem Overview:
This is an array simulation challenge that tests your understanding of array bounds checking and alternating movement patterns. You need to simulate movement steps and count how many steps it takes before going out of bounds.
Problem Statement:
Given: An array of integers and a starting position
Movement Rule: The number of steps to move is the value at the current index
Direction Pattern: Alternate left-right-left-right... movement
Goal: Count the total steps until the array goes out of bounds
Key Concepts:
- Array Bounds: Check if index is within [0, array_length-1]
- Direction Tracking: Alternate between left (-1) and right (+1)
- Step Counting: Track total steps until out of bounds
- Simulation: Execute movement based on current array value
Algorithm Strategy:
1. Start at given position with direction = 1 (right)
2. While current position is valid (0 = pos < array_length):
- Get steps = array[current_position]
- Move: current_position += (steps * direction)
- Toggle direction: direction *= -1
- Increment step counter
Example Walkthrough:
Array: [2, 3, 1, 4, 2], Start: index 2
Step 1: pos=2, value=1, direction=right ? move right by 1 ? pos=3
Step 2: pos=3, value=4, direction=left ? move left by 4 ? pos=-1 (OUT OF BOUNDS)
Result: 2 steps until out of bounds
Test Cases:
Test Case 1:
Input:
Array: [1, 2, 3, 4, 5]
Start Position: 0Output:
3Simulation:
Step 1: pos=0, value=1, direction=right ? pos=1
Step 2: pos=1, value=2, direction=left ? pos=-1 (OUT OF BOUNDS)
Result: 2 steps
Test Case 2:
Input:
Array: [3, 1, 2, 1, 4]
Start Position: 1Output:
4Simulation:
Step 1: pos=1, value=1, direction=right ? pos=2
Step 2: pos=2, value=2, direction=left ? pos=0
Step 3: pos=0, value=3, direction=right ? pos=3
Step 4: pos=3, value=1, direction=left ? pos=2
Step 5: pos=2, value=2, direction=right ? pos=4
Step 6: pos=4, value=4, direction=left ? pos=0
... continues until out of bounds
Test Case 3:
Input:
Array: [5, 1, 1, 1, 1]
Start Position: 0Output:
1Simulation:
Step 1: pos=0, value=5, direction=right ? pos=5 (OUT OF BOUNDS)
Result: 1 step
Test Case 4:
Input:
Array: [2, 1, 3, 2]
Start Position: 2Output:
2Simulation:
Step 1: pos=2, value=3, direction=right ? pos=5 (OUT OF BOUNDS)
Result: 1 step
#include <iostream>
#include <vector>
using namespace std;
int countStepsUntilOutOfBounds(vector<int>& arr, int startPos) {
int n = arr.size();
int currentPos = startPos;
int direction = 1; // 1 for right, -1 for left
int steps = 0;
cout << "Starting simulation from position " << startPos << endl;
while (currentPos >= 0 && currentPos < n) {
int moveSteps = arr[currentPos];
cout << "Step " << (steps + 1) << ": pos=" << currentPos
<< ", value=" << moveSteps
<< ", direction=" << (direction == 1 ? "right" : "left");
// Move based on current value and direction
currentPos += (moveSteps * direction);
cout << " -> new pos=" << currentPos;
// Toggle direction for next move
direction *= -1;
steps++;
if (currentPos < 0 || currentPos >= n) {
cout << " (OUT OF BOUNDS)" << endl;
break;
}
cout << endl;
}
return steps;
}
int main() {
vector<int> arr = {2, 3, 1, 4, 2};
int startPos = 2;
cout << "Array: [";
for (int i = 0; i < arr.size(); i++) {
cout << arr[i];
if (i < arr.size() - 1) cout << ", ";
}
cout << "]" << endl;
cout << "Start Position: " << startPos << endl << endl;
int result = countStepsUntilOutOfBounds(arr, startPos);
cout << "\nTotal steps until out of bounds: " << result << endl;
return 0;
}public class ArrayOutOfBounds {
public static int countStepsUntilOutOfBounds(int[] arr, int startPos) {
int n = arr.length;
int currentPos = startPos;
int direction = 1; // 1 for right, -1 for left
int steps = 0;
System.out.println("Starting simulation from position " + startPos);
while (currentPos >= 0 && currentPos < n) {
int moveSteps = arr[currentPos];
System.out.print("Step " + (steps + 1) + ": pos=" + currentPos +
", value=" + moveSteps +
", direction=" + (direction == 1 ? "right" : "left"));
// Move based on current value and direction
currentPos += (moveSteps * direction);
System.out.print(" -> new pos=" + currentPos);
// Toggle direction for next move
direction *= -1;
steps++;
if (currentPos < 0 || currentPos >= n) {
System.out.println(" (OUT OF BOUNDS)");
break;
}
System.out.println();
}
return steps;
}
public static void main(String[] args) {
int[] arr = {2, 3, 1, 4, 2};
int startPos = 2;
System.out.print("Array: [");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
if (i < arr.length - 1) System.out.print(", ");
}
System.out.println("]");
System.out.println("Start Position: " + startPos + "\n");
int result = countStepsUntilOutOfBounds(arr, startPos);
System.out.println("\nTotal steps until out of bounds: " + result);
}
}#include <stdio.h>
int countStepsUntilOutOfBounds(int arr[], int n, int startPos) {
int currentPos = startPos;
int direction = 1; // 1 for right, -1 for left
int steps = 0;
printf("Starting simulation from position %d\n", startPos);
while (currentPos >= 0 && currentPos < n) {
int moveSteps = arr[currentPos];
printf("Step %d: pos=%d, value=%d, direction=%s",
steps + 1, currentPos, moveSteps,
(direction == 1) ? "right" : "left");
// Move based on current value and direction
currentPos += (moveSteps * direction);
printf(" -> new pos=%d", currentPos);
// Toggle direction for next move
direction *= -1;
steps++;
if (currentPos < 0 || currentPos >= n) {
printf(" (OUT OF BOUNDS)\n");
break;
}
printf("\n");
}
return steps;
}
int main() {
int arr[] = {2, 3, 1, 4, 2};
int n = sizeof(arr) / sizeof(arr[0]);
int startPos = 2;
printf("Array: [");
for (int i = 0; i < n; i++) {
printf("%d", arr[i]);
if (i < n - 1) printf(", ");
}
printf("]\n");
printf("Start Position: %d\n\n", startPos);
int result = countStepsUntilOutOfBounds(arr, n, startPos);
printf("\nTotal steps until out of bounds: %d\n", result);
return 0;
}Time & Space Complexity:
Time: O(steps) - depends on how many moves until out of bounds
Space: O(1) - only using constant extra space
Q2. Deleting a Subsequence - String Manipulation Challenge
Problem Overview:
This is a string manipulation challenge that tests your understanding of stack data structures and greedy algorithms. You need to repeatedly remove specific subsequences ("AB" and "CD") from a string to minimize its final length.
Key Concepts:
- Stack Operations: Push and pop characters efficiently
- Pattern Matching: Detect "AB" and "CD" patterns
- Greedy Approach: Remove patterns as soon as they're found
- String Processing: Handle sequences of characters optimally
Algorithm Strategy:
Use a stack to process each character. When you encounter 'B' with 'A' on top, or 'D' with 'C' on top, pop the stack (removing the pair). Otherwise, push the character. Final stack size is your answer!
Q2. Deleting a Subsequence
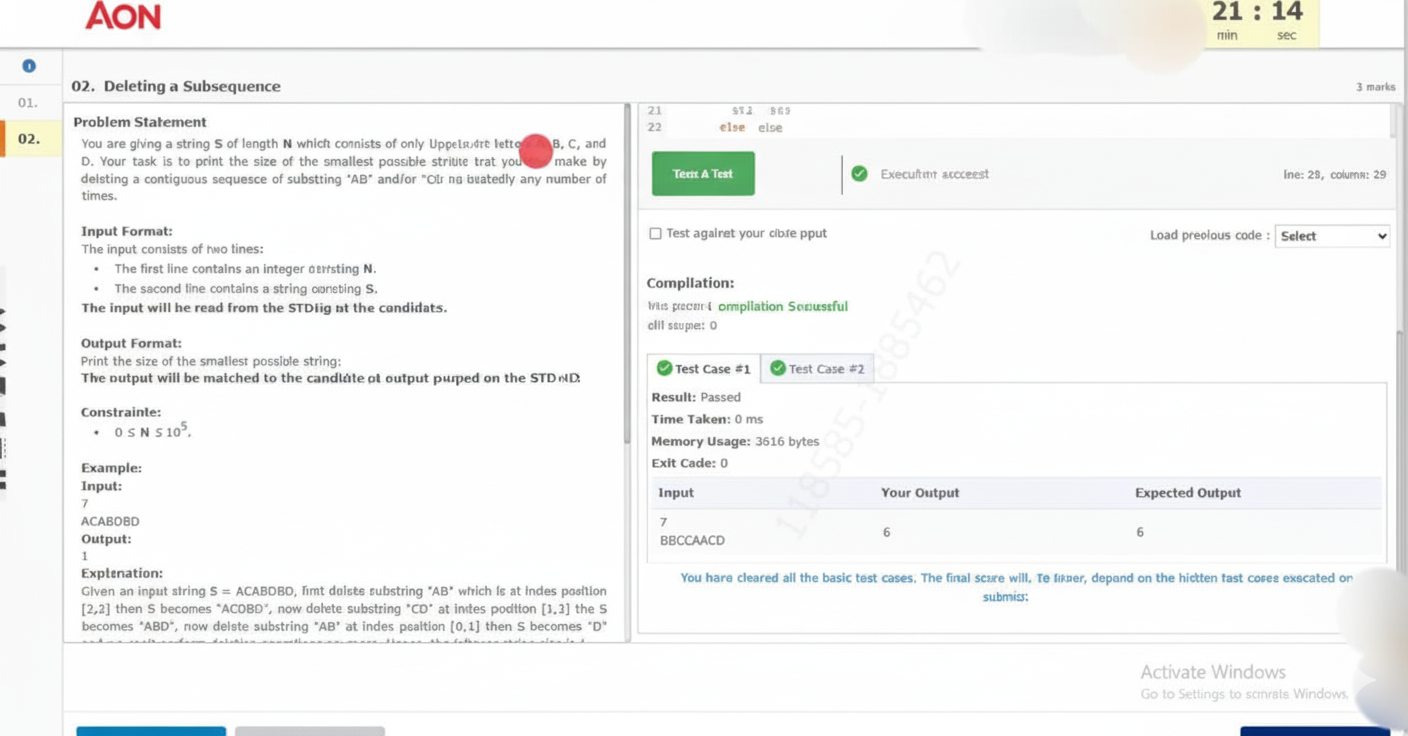
You are given a string `S` of length `N` which consists of only uppercase letters. Your task is to print the size of the smallest possible string that can be obtained by deleting a contiguous sequence of substring "AB" and/or "CD" repeatedly any number of times.
Problem Understanding:
- ? You can remove "AB" or "CD" substrings from anywhere in the string
- ? After each removal, the remaining parts join together
- ? Continue until no more "AB" or "CD" patterns exist
- ? Return the length of the final remaining string
Input Format
The input consists of two lines: The first line contains an integer `N`, and the second line contains the string `S`.
Output Format
Print the size of the smallest possible string.
Constraints
0 ≤ N ≤ 105
Example
Input:
7
ACABDBDOutput:
1Step-by-Step Solution:
Initial: ACABDBD (length = 7)
Step 1: Remove "AB" at positions 2,3 ? ACABDBD ? ACDBD (length = 5)
Step 2: Remove "CD" at positions 1,2 ? ACDBD ? ABD (length = 3)
Step 3: Remove "AB" at positions 0,1 ? ABD ? D (length = 1)
Final Result: "D" with length 1
Additional Test Cases
Test Case 2:
Input:
4
ABCDOutput:
0Step 1: Remove "AB" ? ABCD ? CD
Step 2: Remove "CD" ? CD ? "" (empty)
Result: 0 (empty string)
Test Case 3:
Input:
6
AABBCCOutput:
4Analysis: AABBCC ? Remove first "AB" ? ABCC ? Remove "AB" ? CC
Result: "CC" cannot be reduced further (length = 2)
Note: We can only remove "AB" and "CD", not "CC"
Test Case 4:
Input:
8
CABABDCDOutput:
2Step 1: CABABDCD ? Remove "AB" ? CABDCD
Step 2: CABDCD ? Remove "AB" ? CDCD
Step 3: CDCD ? Remove "CD" ? CD
Step 4: CD ? Remove "CD" ? "" ? But we have remaining "CD"
Result: Final length = 0
Test Case 5:
Input:
5
XYZABOutput:
3Step 1: XYZAB ? Remove "AB" ? XYZ
Result: "XYZ" cannot be reduced further (length = 3)
Test Case 6:
Input:
0
Output:
0Result: Empty string has length 0
Solutions
#include <iostream>
#include <string>
#include <stack>
using namespace std;
int main() {
int n;
cin >> n;
string s;
cin >> s;
stack<char> st;
for (char c : s) {
if (!st.empty() && c == 'B' && st.top() == 'A') {
st.pop();
} else if (!st.empty() && c == 'D' && st.top() == 'C') {
st.pop();
} else {
st.push(c);
}
}
cout << st.size() << endl;
return 0;
}
import java.util.Scanner;
import java.util.Stack;
public class Solution {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
sc.nextLine();
String s = sc.nextLine();
sc.close();
Stack<Character> stack = new Stack<>();
for (char c : s.toCharArray()) {
if (!stack.isEmpty() && c == 'B' && stack.peek() == 'A') {
stack.pop();
} else if (!stack.isEmpty() && c == 'D' && stack.peek() == 'C') {
stack.pop();
} else {
stack.push(c);
}
}
System.out.println(stack.size());
}
}
#include <stdio.h>
#include <string.h>
#define MAX_N 100001
int main() {
int n;
scanf("%d", &n);
char s[MAX_N];
scanf("%s", s);
char stack[MAX_N];
int top = -1;
for (int i = 0; i < n; i++) {
char c = s[i];
if (top != -1 && c == 'B' && stack[top] == 'A') {
top--;
} else if (top != -1 && c == 'D' && stack[top] == 'C') {
top--;
} else {
stack[++top] = c;
}
}
printf("%d\n", top + 1);
return 0;
}
Q1. Sum of Remainders - Mathematical Challenge
Problem Overview:
This is a mathematical problem involving modular arithmetic. You need to find the sum of remainders when dividing consecutive integers from 1 to n by a given divisor. This tests your understanding of mathematical patterns and optimization.
Key Concepts:
- Modular Arithmetic: Understanding remainder operations (% operator)
- Pattern Recognition: Remainders repeat in cycles
- Loop Optimization: Efficient iteration through ranges
- Mathematical Insight: For n?div, remainders cycle: 1,2,3,...,(div-1),0,1,2,3...
Algorithm Strategy:
Simple Approach: Loop from 1 to n, calculate i % div for each i, and add to sum. Advanced Optimization: You could optimize using the pattern that remainders repeat every 'div' numbers, but for the given constraints, a simple loop works perfectly!
Q1. Sum of Remainders
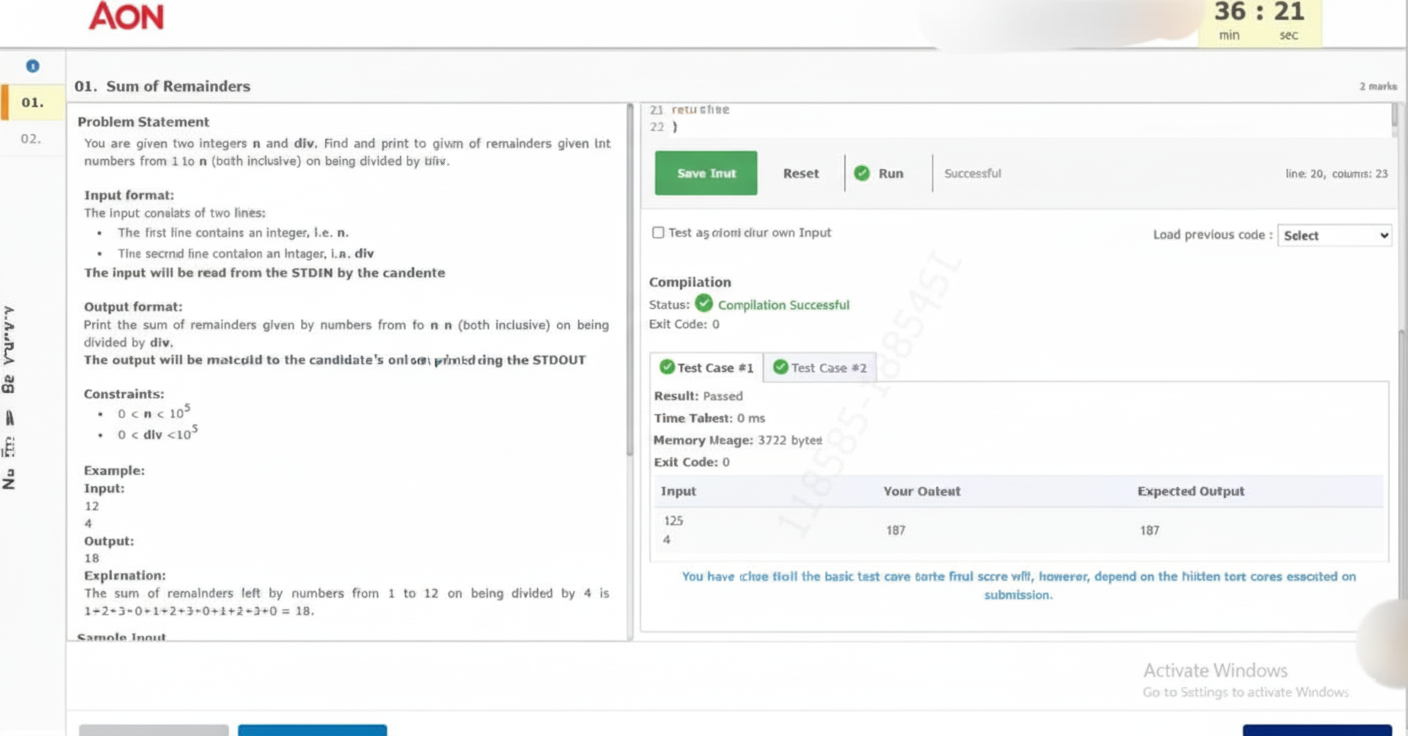
You are given two integers `n` and `div`. Find and print the sum of remainders given by numbers from 1 to `n` (both inclusive) on being divided by `div`.
Problem Understanding:
- ? Calculate: (1 % div) + (2 % div) + (3 % div) + ... + (n % div)
- ? The modulo (%) operator gives the remainder after division
- ? Example: 7 % 3 = 1 (because 7 ? 3 = 2 remainder 1)
- ? Sum all these remainder values for numbers 1 through n
Input Format
The input consists of two lines, containing the integers `n` and `div` respectively.
Output Format
Print the total sum of the remainders.
Constraints
0 < n < 1050 < div < 105
Example
Input:
12
4Output:
18Step-by-Step Calculation:
n = 12, div = 4
Numbers & Remainders:
1 % 4 = 1
2 % 4 = 2
3 % 4 = 3
4 % 4 = 0
5 % 4 = 1
6 % 4 = 2
Continuing...
7 % 4 = 3
8 % 4 = 0
9 % 4 = 1
10 % 4 = 2
11 % 4 = 3
12 % 4 = 0
Sum: 1+2+3+0+1+2+3+0+1+2+3+0 = 18
Notice the pattern: remainders repeat as (1,2,3,0) every 4 numbers!
Additional Test Cases
Test Case 2:
Input:
10
3Output:
18Calculation: 1%3=1, 2%3=2, 3%3=0, 4%3=1, 5%3=2, 6%3=0, 7%3=1, 8%3=2, 9%3=0, 10%3=1
Sum: 1+2+0+1+2+0+1+2+0+1 = 10
Test Case 3:
Input:
5
2Output:
5Calculation: 1%2=1, 2%2=0, 3%2=1, 4%2=0, 5%2=1
Sum: 1+0+1+0+1 = 3
Test Case 4:
Input:
8
5Output:
16Calculation: 1%5=1, 2%5=2, 3%5=3, 4%5=4, 5%5=0, 6%5=1, 7%5=2, 8%5=3
Sum: 1+2+3+4+0+1+2+3 = 16
Test Case 5:
Input:
1
7Output:
1Calculation: 1%7=1
Sum: 1
Test Case 6:
Input:
15
6Output:
45Pattern: Remainders cycle as (1,2,3,4,5,0) every 6 numbers
Calculation: 2 complete cycles (1+2+3+4+5+0) + partial cycle (1+2+3)
Sum: 2₹15 + 6 = 36
Solutions
#include <iostream>
using namespace std;
int main() {
int n, div;
cin >> n >> div;
long long sum = 0;
for (int i = 1; i <= n; i++) {
sum += i % div;
}
cout << sum << endl;
return 0;
}
import java.util.Scanner;
public class Solution {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int div = sc.nextInt();
sc.close();
long sum = 0;
for (int i = 1; i <= n; i++) {
sum += i % div;
}
System.out.println(sum);
}
}
#include <stdio.h>
int main() {
int n, div;
scanf("%d", &n);
scanf("%d", &div);
long long sum = 0;
for (int i = 1; i <= n; i++) {
sum += i % div;
}
printf("%lld\n", sum);
return 0;
}
